वृत्त का क्षेत्रफल द्वि-आयामी विमाए में वृत्त द्वारा घिरा हुआ वह क्षेत्र है, जो वृत्त के परिधि से व्यस्त रहता है. फार्मूला के प्रयोग से क्षेत्रफल सरलता से निर्धारित किया जा सकता है. दरअसल, Vritt Ka Kshetrafal का प्रयोग एक गोलाकार क्षेत्र या भूखंड से घिरे हुए स्थान को मापने के लिए किया जाता है.
परिस्थित के अनुसार वृत्त का क्षेत्रफल का प्रयोग विभिन्न प्रकार के प्रश्नों को हल करने के लिए किया जाता है. जैसे वृत्त को रंगने में लगे कुल लागत, क्षेत्रफल, प्रतिसत वाले प्रश्न, वृत्त द्वारा घेरा गया क्षेत्रफल आदि.
सरकारी एग्जाम एवं बोर्ड परीक्षा में वृत्त का प्रयोग अधिक होता है. इसलिए, Vritt Ka Kshetrafal का अहिमियत अधिक है. शिक्षक के निर्धेशानुसार वृत्त का फार्मूला सबसे उपयोगी है क्योंकि सभी तरह के एग्जाम में इस टॉपिक से प्रश्न पूछे जाते है. अतः वृत्त के क्षेत्रफल के साथ-साथ इसके महत्वपूर्ण भागो के विषय में भी अध्ययन करेंगे. जो यहाँ प्रदर्शित है.
वृत्त का क्षेत्रफल का परिभाषा
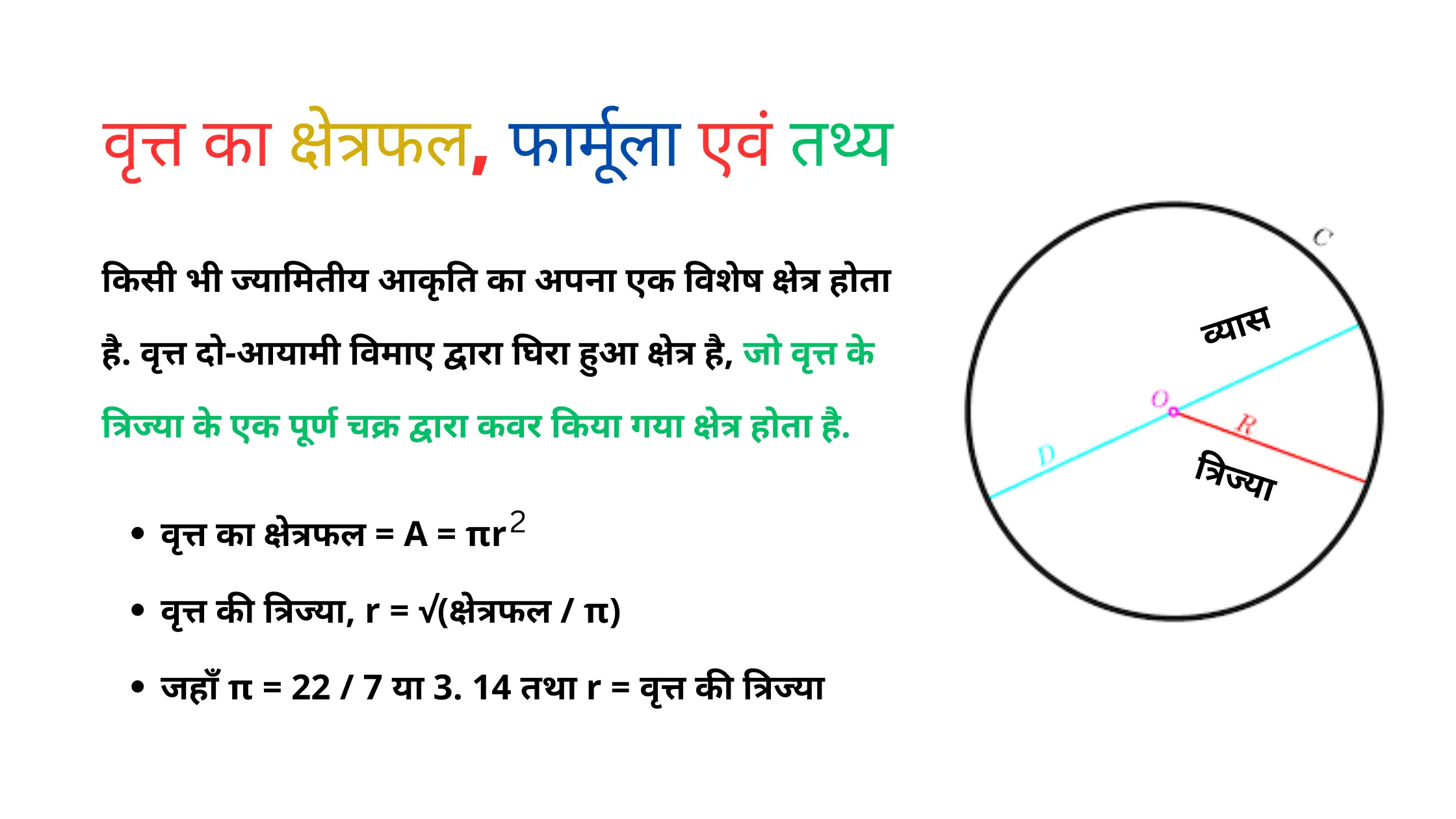
किसी भी ज्यामितीय आकृति का अपना एक विशेष क्षेत्र होता है जिसमे से एक वृत्त है. यह दो-आयामी विमाए द्वारा घिरा हुआ क्षेत्र है, जो वृत्त के त्रिज्या के एक पूर्ण चक्र द्वारा कवर किया गया क्षेत्र होता है. उसे वृत्त का क्षेत्रफल कहते है.
एक वृत्त का क्षेत्रफल मुख्यतः को दो तरीकों का उपयोग करके सिद्ध किया जा सकता है. जैसे;
- आयतों के प्रयोग से
- त्रिभुज के प्रयोग से
वृत्त का क्षेत्रफल = πr2, अर्थात = π×r×r जहाँ π = 22 / 7 या 3.14
Note:
यह सिद्ध किया हुआ विवरण है जो हमारे गणितज्ञों द्वारा प्रतिस्थापित किया गया है.
वृत्त की परिभाषा यूक्लिड के अनुसार
वृत्त एक बंधरेखा से घिरी हुई एक समतलीय आकृति है, और यह इस तरह होता है कि किसी निश्चित बिंदु इस बंधरेखा तक की सभी रेखाएं लंबाई में बराबर होता हैं। यह बंधरेखा, इस वृत्त की परिधि और निश्चित बिंदु, इसका केंद्र कहलाता है
यूक्लिड
वृत्त का व्यास
वृत्त का व्यास वह रेखाखंड है जो वृत्त को दो समान भागों में विभाजित करता है जिसे वृत्त की सबसे बड़ी जीवा भी कहा जाता है. दुसरें शब्दों में यह वृत्त की त्रिज्या का केवल दोगुना ही होता है. यह वृत्त के किसी भी दो बिन्दुओं बिच की सबसे बड़ी दुरी होती है.
मुख्यरूप से, इसे D या Diameter द्वारा सूचित किया जाता है.
वृत्त की त्रिज्या
Vrit की त्रिज्या वह रेखा है जो वृत्त के केंद्र को बाहरी सीमा से जोड़ती है. अर्थात, वृत्त के केंद्र से वृत्त की परिधि के किसी भी बिंदु तक का एक रेखाखंड, त्रिज्या कहलाता है. इसे “r” या “R” ’द्वारा दर्शाया जाता है
क्षेत्रफल और वृत्त की परिधि के सूत्र में, त्रिज्या एक महत्वपूर्ण भूमिका होती है, जिसका अध्ययन बाद में विस्तार से करेंगे.
जीवा (Chord)
वह रेखाखंड, जो वृत्त के दो बिन्दुओं को मिलाने से प्राप्त होता है, उसे जीवा कहा जाता है.
Note:
वृत्त के क्षेत्रफल में जितने भागों की आवश्यकता है उन्हें ही यहाँ सामिल किया गया है.
वृत्त का क्षेत्रफल का फार्मूला
क्लास 5th से क्लास 12th तक के प्रशों में इसी वृत्त का क्षेत्रफल का प्रयोग होता है. केवल इसके प्रश्न पूछने के तरीके बदल जाते है लेकिन फार्मूला एक ही होता है. इसलिए, इस फार्मूला का अध्ययन आवश्यक है.
वृत्त का क्षेत्रफल = A = πr2 या πd2/4
जहाँ π = 22 / 7 या 3. 14 तथा r = वृत्त की त्रिज्या
वृत्त की त्रिज्या, r = √(क्षेत्रफल / π)
वृताकार वलय का क्षेत्रफल = π (R2 – r2)
वृत्त के क्षेत्रफल का प्रयोग:
- यदि किसी वृत्त की त्रिज्या में x % की वृद्धि की जाए, तो परिधि में x % तथा क्षेत्रफल में (2 x + x2/100)% की वृद्धि होती है.
- किसी वृत्त की त्रिज्या में x % की कमी की जाए, तो परिधि में x % तथा क्षेत्रफल में (2 x – x2/100)% की कमी होती है.
वृत्त के क्षेत्रफल का उदाहरण
1. यदि किसी वृत्त की त्रिज्या 10% कम कर दी जाए तो, उसका क्षेत्रफल कितना % कम होगा?
हल: माना वृत्त की त्रिज्या = x और x = 10
इसलिए, वृत्त के क्षेत्रफल में कमी = (2 x – x2/100)%
=> 2 × 10 – (10 × 10) / 100
=> 20 – 1 => 19
अर्थात वृत्त के क्षेत्रफल में 19 % की कमी होगी.
2. यदि वृत्त का क्षेत्रफल 154 cm2 हो, तो वृत्त की त्रिज्या निकले?
हल: दिया है, वृत्त का क्षेत्रफल = 154 cm2
फार्मूला से = πr2
चूँकि => πr2 = 154
अर्थात, => r2 = 154 / π => r = √ (154 × 7)/22
=> r = √ (154 × 7)/22 => √ 77 cm2
3. किसी वृत्त का व्यास 6 cm, तो वृत्त का क्षेत्रफल क्या होगा?
हल: दिया है, व्यास = 6 cm, इसलिए त्रिज्या = 6/2 = 3
सूत्र से, = πr2
=> 22/7 × 3 × 3 = 28.6 cm2
FAQs
वृत्त का क्षेत्रफल πr2, जहाँ π = 22 / 7 या 3.14 होता है.
वृत्त के केंद्र पर 360° का कोण बनता होता है.
वह ज्यामितीय आकृति जो दो-आयामी विमाओ से घिरा हुआ हो, जो वृत्त के त्रिज्या के एक पूर्ण चक्र द्वारा कवर किया गया क्षेत्र है. उसे वृत्त का क्षेत्रफल कहते है.
सम्बंधित पोस्ट: