अलजेब्रा फार्मूला यानि बीजगणित सूत्र का प्रयोग गणित में सामान्य एवं उच्च स्तर पर किया जाता है ताकि गणित की गणना सावधानी से किया जा सके. सभी आवश्यक जरूरतों को ध्यान में रखते हुए अलजेब्रा यानि बीजगणित की सभी फार्मूला को यहाँ ध्यानपूर्वक सजाया गया है जिससे किसी भी तरह के प्रश्न हल करने में प्रयोग की जाने वाली फार्मूला का उपयोग निसंदेह किया सके.
बीजगणितीय फार्मूला एक ऐसी जरुरत है जिसका प्रयोग लगभग गणित के सभी भागों में किया जाता है और इसी के बदौलत प्रश्न हल करने में सहूलियत मिलती है. इसलिए इस अध्याय यानि फार्मूला के विषय में जानकारी रखना प्रत्येक विद्यार्थी की सर्वप्रथम जिम्मेदारी है. आइए बीजगणित सूत्र का अध्ययन विस्तार से करते है:
बीजगणित सूत्र
यहाँ सभी अलजेब्रा सूत्र को एक साथ अंकित किया जा रहा है जिसका प्रयोग लगभग प्रत्येक प्रश्न को हल करने में किया जाता है. यह आपके कौशल को बढ़ाने में आन्तरिक उर्जा प्रदान करते है जिससे आपके गणित के अध्ययन में एक नया कीर्तिमान जुड़ जाता है.
इसकी उपयोगितायों को अनदेखा नही किया जा सकता है अन्यथा आप गणित जैसे विषय की जानकरी से वंचित रह सकते है. विद्वानों का परामर्श है कि बीजगणित गणित की पहली इकाई है और यही आपकी पहली अध्याय भी होती है. इसलिए अलजेब्रा फार्मूला पूर्ण करना आपका प्रथम कर्तव्य होता है.
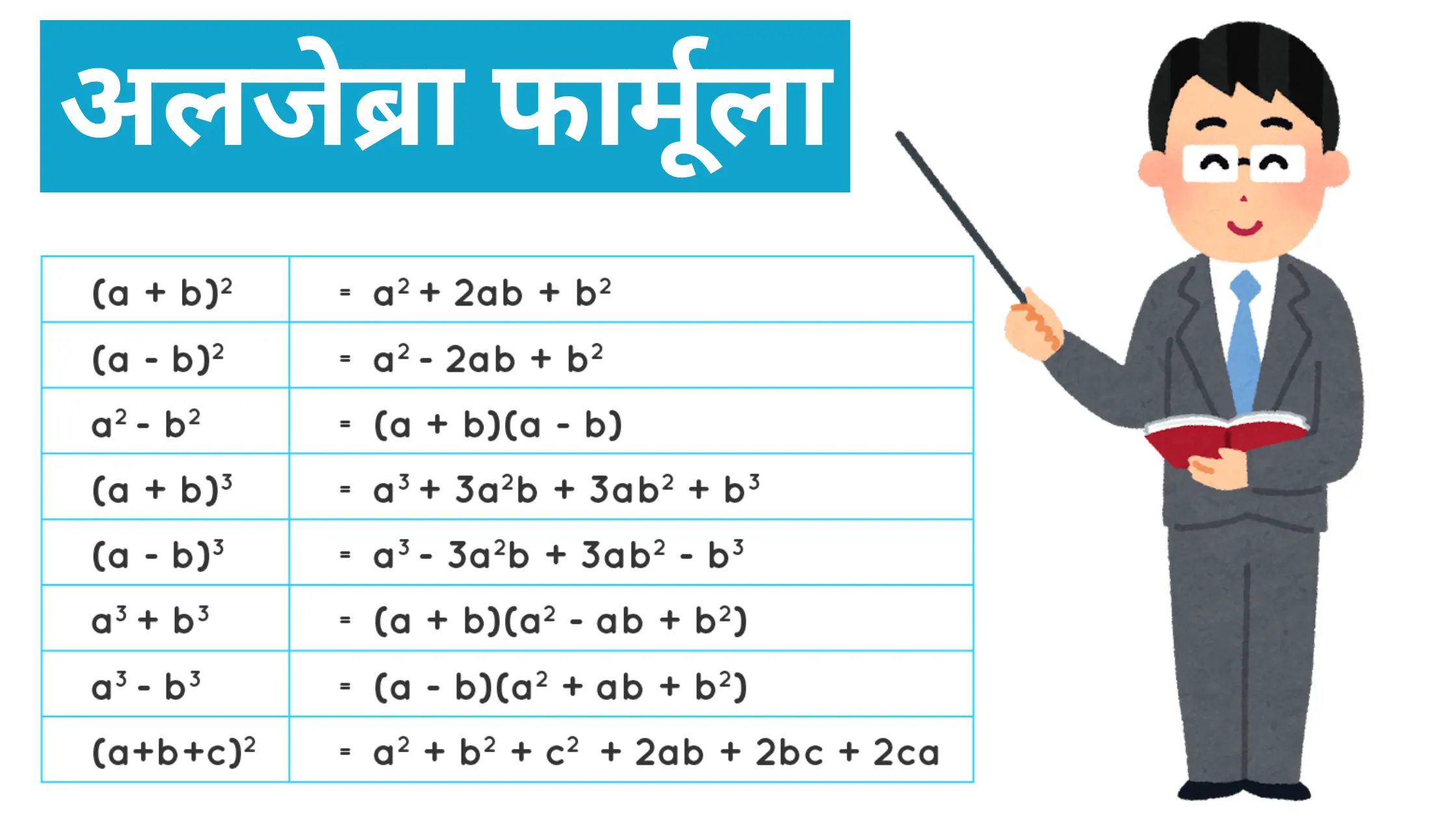
अलजेब्रा फार्मूला चार्ट
a2 – b2 = (a – b)(a + b)
(a+b)2 = a2 + 2ab + b2 Or a2 + b2 + 2ab
a2 + b2 = (a – b)2 + 2ab Or (a + b)2 – 2ab
(a – b)2 = a2 – 2ab + b2 Or a2 + b2 – 2ab
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
(a – b – c)2 = a2 + b2 + c2 – 2ab – 2ac + 2bc
(a + b)3 = a3 + 3a2b + 3ab2 + b3 ; (a + b)3 = a3 + b3 + 3ab(a + b)
(a – b)3 = a3 – 3a2b + 3ab2 – b3 Or a3 – b3 – 3ab ( a – b)
a3 – b3 = (a – b)(a2 + ab + b2) Or (a – b)3 + 3ab ( a – b ) Or ( a – b ) ( a2 + ab + b2 )
a3 + b3 = (a + b)(a2 – ab + b2) Or (a + b)3 – 3ab ( a + b )
(a + b)3 = a3 + 3a2b + 3ab2 + b3 Or a3 + b3 + 3 ab ( a + B )
(a – b)3 = a3 – 3a2b + 3ab2 – b3 Or a3 – b3 – 3 ab ( a – B )
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4)
(a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4)
a4 – b4 = (a – b)(a + b)(a2 + b2)
a5 – b5 = (a – b)(a4 + a3b + a2b2 + ab3 + b4)
अलजेब्रा स्क्वायर सूत्र
- (a + b) 2 = a 2 + b 2 + 2ab Or (a − b) 2 + 4 ab
- (a − b) 2 = a 2 + b 2 − 2ab Or (a + b) 2 − 4 ab
- a 2 − b 2 = (a − b) (a + b)
- (x + a) (x + b) = x 2 + (a + b) x + ab
- (a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca
- (a + (−b) + (−c))2 = a2 + (−b)2 + ( −c )2 + 2a(−b) + 2(−b) (−c) + 2a (−c)(a – b – c)2 = a 2 + b 2 + c 2 − 2ab + 2bc − 2ca
बीजगणित क्यूब सूत्र
- (a + b) 3 = a 3 + b 3 + 3ab(a + b)
- (a − b) 3 = a 3 – b 3 – 3ab(a – b)
- a 3 − b 3 = (a − b) (a 2 + b 2 + ab)
- a 3 + b 3 = (a + b) (a 2 + b 2 − ab)
- (a + b + c) 3 = a 3 + b 3 + c 3 + 3(a + b)(b + c)(c + a)
- a 3 + b 3 + c 3 − 3abc = (a + b + c) (a 2 + b 2 + c 2 − ab − bc − ac)
- जहाँ a + b + c = 0 हो, तो a 3 + b 3 + c 3 = 3abc
घातांक के महत्वपूर्ण नियम
यह बीजगणित का ही एक भाग होता है. विशेषज्ञों के अनुसार जहाँ भी अलजेब्रा फार्मूला का प्रयोग होता है वहां घातांक के नियम का भी प्रयोग किया जाता है. इसलिए आवश्यक है कि आपको घातांक महत्वपूर्ण नियमों के विषय में कुछ ज्ञात हो.
1. (am)(an) = am+n
2. (ab)m = ambm
3. (am)n = amn
आंशिक घातांक के महत्वपूर्ण नियम
यह नियम विशेष कर बीजगणित में इस्तेमाल किया जाता है.
- √a = a 1/2
- ∛a = a 1/3
- n √a = a 1/n
- a p . a q = a p + q
घातांक के भाग का नियम
- (ap ) / (a q ) = a p – q
- ap . bp = ( a . b ) p
- (a p ) q = a pq
- a 0 = 1
- a –n = 1/a n
शरांश
जरुरी नही, ऊपर दिए हुए सभी Algebra Formulas को आप रटकर याद करे, बल्कि फार्मूला अनुसार प्रश्न हल कर सरलता से सभी नियम याद कर सकते है. हमारी टीम विधार्थियों के लिए सरल एवं सुविधाजनक तथ्यों को प्रस्तुत करती है ताकि विद्यार्थी ऐसी परेशानी से बाहर निकल सके. आपसे आग्रह है कि अलजेब्रा फार्मूला के तथ्यों का मूल्यांकन करने से परेशानी खुद व खुद हल हो जाएगी.